Начнем с вращения в классической механике. Вот есть известный пример, с помощью которого иллюстрируют закон сохранения момента импульса вращающегося тела и роль момента инерции. Фигурист на льду быстро вращается, прижав руки к телу, но как только он их разведет в стороны, скорость его вращения сильно замедляется, хотя его момент импульса почти не изменился. Так получается потому, что момент импульса — это не просто угловая скорость вращения, это момент инерции помножить на угловую скорость. Как только вы разводите руки в стороны, вы резко увеличиваете момент инерции, значит, угловая скорость должна упасть.
Теперь следующий пример, совсем близко к нашему «парадоксу». Возьмем планету на круговой орбите вокруг Солнца. Поступательная скорость его движения по орбите (первая космическая) и его угловая скорость равны
А момент импульса есть
То есть, если вы переведете ту же планету на более высокую круговую орбиту, то угловая скорость уменьшится, но момент импульса увеличится, и, как видите, никакого парадокса тут нет.
Теперь о том, что происходит с закрученной волной. Для простоты забудем про поляризацию, она на сущность «парадокса» не влияет. И еще будем рассматривать совсем простой вариант закрученной волны — так называемый бесселев пучок. Он представляет из себя суперпозицию плоских волн, приходящих под одинаковыми полярными углами, но под разными азимутальными углами к оси z, ну и с правильной настройкой относительных фаз. Бесселевы пучки хоть и менее физичны, чем лагерр-гауссовы пучки, которые обычно в этих задачах рассматриваются, но они проще для изучения и иллюстрации.
Так вот, волновая функция бесселева пучка в поперечной плоскости (полярные координаты R и φ) имеет такой вид:
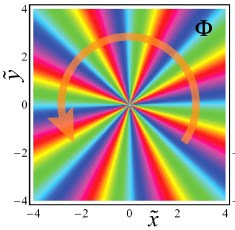 |
| Рис. 1. Фаза закрученной волны с m=8 в поперечной плоскости (источник изображения) |
А теперь посмотрим на формулу внимательнее и заметим, что значение m влияет не только на угловую зависимость, но и на радиальную, ведь там стоит бесселева функция именно m-го порядка. Как выглядит график бесселевой функции для разных m? Для примера на рис. 2 нарисован квадрат функций J2(x) и J20(x).
 |
| Рис. 2. Графики квадратов J2(x) и J20(x). |
Пользуясь механической аналогией, можно сказать, что с ростом m, у пучка словно увеличивается момент инерции (для чисто бесселевого пучка это некорректное заявление, но это уже мелочи). Да, при этом скорость вращения замедляется, но этот момент инерции с лихвой компенсирует это замедление. И в результате орбитальный угловой момент растет пропорционально m как раз за счет этой «перекомпенсации» (формулы для механической аналогии написать совсем несложно).
Такая вот небольшая тонкость.


Скажите пожалуйста,а фотон создаёт гравитационное
ОтветитьУдалитьполе? и "гонит" ли он гравитационную волну и если он закручен,то гравитационная волна тоже закручена?
Знаете, здесь столько тонкостей (начиная с обсуждения того, что такое «фотон» и что такое «луч света», и заканчивая объяснением, почему два параллельных луча света не взаимодействуют гравитационно, а непараллельных — взаимодействуют), что я за разумное время не смогу написать краткий, понятный и полностью правильный ответ. В любом случае, вы задаете вопрос про нереальный для экспериментального наблюдения эффект, по крайней мере в ближайшие столетия. Пока что не нашли грав.волн от слияния двух вращающихся нейтронных звезд, не говоря уже от движении «земных» макроскопических объектов и уж тем более не говоря об отдельных фотонах.
УдалитьИгорь. Вопрос такой. Уменьшается ли скорость света из-за закрутки?
ОтветитьУдалитьЕсли следовать логическим рассуждениям, то скорость распространения волнового фронта равна с. Но из за того, что волновой фронт расположен под углом к направлению движения, то скорость равно с*cosA, где А - угол наклона. Т.е. можно сказать что фронт распространяется со скоростью С, но не по прямой, а по винтовой траектории, следовательно проходит от точки А до точки Б больший путь нежели кратчайшая прямая, тратя при этом больше времени.
Теперь дальше. Угол наклона зависит от расстояния от центра светогого фронта (по аналогии с пропеллером). В пределе в центре угол поворота фронта волны должен достигать 90 градусов, а скорость света должна упасть до нуля. Другими словами, центр фронта световой волны должен отставать по скорости от переферии.
Получаются как колечки дыма (только там обычно наоборот - поток воздуха в центре выше). Кстати, не этим ли вызваны колечки на дифракционной картинке закрученного света? Серединка просто вываливается из-за отставания в скорости. И чем болше закрутка, тем сильнее вырезается серединка.
ovz
На Элементах есть задачка на эту тему: http://elementy.ru/problems/288
УдалитьЕсли кратко, то фазовая скорость больше c, групповая меньше c, их произведение равно c^2.
Вы всё нормально написали вплоть до момента про сердцевину. Она не отстает, вся волна бежит вперед с одинаковой скоростью, там нет никакого отставания, по крайней мере для бесселевых пучков, которые служат базисными состояниями. А в суперпозиции вы можете приготовить, что угодно, но это уже будет особенность суперпозиции, а не закрученного света.
Игорь, а есть ли установившаяся терминология для волн с орбитальным угловым моментом в русском языке? В английском - twisted wave. А в русском слово "закрученная" выделяют скобочками как жаргонизм.
ОтветитьУдалитьХотя история развития языка говорит, что скобочки постепенно исчезают. Вы вот, например, уже их практически перестали ставить.
Twisted широко распространено в популярных новостях, а непосредственно в статьях пишут vortex states, vortex beams. И бывает даже рецензенты или редакторы просят авторов заменить twisted на vortex.
УдалитьНа русском установившегося термина я не знаю, но думаю, что его и нет. Просто на эту тему да еще по-русски статьи пишутся наверно очень редко, а те, кто пишут, наверняка сами гадают, как правильнее, так что пока ничего и не установилось. Даже если сейчас больше пишут «закрученные», то я думаю, постепенно перейдут на «вихревые». В научпопе - там да, «закрученные» или «скрученные», но это просто копирование twisted.
Может быть, если "приблизиться к академическому языку", называть их спиралевидными (со спиралевидным фронтом), или геликоидальными? Последнее название не очень подходит, т.к. могут спутать с геликонами в магнитоактивной плазме и металлах.
УдалитьНемного "пошерстил" по англоязычным статья. В самом деле, у них наблюдается динамика к vortex, хотя буквально 6 лет назад и ранее распространено было twisted (взять, хотя бы, книжку Торреса "Twisted Light").
УдалитьДумаю, с терминологией в сингулярной оптике уже многое предложено, например здесь M.S. SOSKIN, M.V. VASNETSOV, “SINGULAR OPTICS”, PROGRESS IN OPTICS 42, 219-276 (2001).
ОтветитьУдалитьА есть ли линейное движение, отдельно взятого фотона?
ОтветитьУдалитьВопрос непонятен. Что вы имеете в виду под линейным движением отдельно взятого фотона? Какую именно характеристику?
УдалитьИз точки "А", в точку "В" "вылетел?" протон "Х". Вопрос : " Что прилетело в точку "В"? Х; Х1; Х2..........
ОтветитьУдалитьФотон не вылетает из точки А. Для фотона неприменимо понятие, что он находится в какой-то точке.
УдалитьЭто образ. Какая энергия приходит в конечную точку.Вообще это очень похоже на принцип "эстафеты", пока предыдущий не завершит круг (оборот), последующий не может принять палочку (энергию) и т.д.
УдалитьВсё, на этом вы отходите от физики и разговариваете про образы, про «наукообразную беллетристику». Физического или математического вопроса тут нет. Если хотите ответ, вернитесь обратно на физическую колею.
УдалитьСуществует ли связь между "закрученными" волнами и волной " шепчущей галереи", скажем, в цилиндрическом волноводе? Эффект шепчущей галереи состоит в локализации волны с "большим угловым моментом" у стенок волновода, известен в акустике ( исследован лордом Рэлеем), оптике, даже в нейтронной физике.
ОтветитьУдалитьАлексей, я хотел вам написать письмо, но что-то ваши емайлы, которые я смог отыскать, не работают.
УдалитьНа днях в Nature вышла статья, где бодро рапортуется о создании закрученных нейтронов с помощью спиральных фазовых пластинок:
http://www.nature.com/nature/journal/v525/n7570/full/nature15265.html
Это некоторый обман, потому что там поперечная когерентность нейтронов очень плохая, так что никакого закрученного волнового фронта у них нет даже близко. Но вы вашим методом смогли бы создать очень чистое состояние по ОУМ, настоящие закрученные нейтроны, и это было бы здорово.
Эффект шепчущей галереи, как в акустике, так и для нейтронов, насколько я понимаю, предполагает, что у вас есть более-менее локализованный волновой пакет, который распространяется по стеночкам. Это явление нестационарное — пространственное распределение плотности звуковой энергии или плотности вероятности нейтрона меняется со временем. В закрученном свете ситуация стационарная: это монохроматическая волна, так что распределение интенсивности в пространстве от времен не зависит.
ОтветитьУдалитьТак, конечно, тоже можно сделать и для звука и для нейтронов, но только это уже будет не шепчущая галерея, а простой волновод с круглым сечением, в котором возбудили определенную радиальную и угловую моду колебания. Тогда да, аналогию проводить можно. Но только эта аналогия в одном существенно отличается: в волноводе распространение волны формируется стенками, т.е. гранусловиями, а закрученный свет распространяется без стенок, просто в вакууме.
Насколько я понял, и в закрученных волнах речь идет о волновых пакетах, которые радиально стационарны лишь приближенно, Это так?
УдалитьЧто для приложений наиболее ценно- стационарность закрученной волны или собственно хорошо определенный угловой момент?
Нет, там именно чистое угловое состояние, не пакет. Если вы таким лучом посветите на экран, то интенсивность будет неизменна во времени. К координатной волновой функции, написанной выше, просто припишите фактор e^{-i omega t}. Если это бесселево состояние, то оно будет к тому же неизменно и вдоль оси z.
УдалитьРазумеется, из них можно делать и пакеты, организуя суперпозицию состояний с разным L, и тогда получатся угловые пакеты, которые будут вращаться. Но можно получать и состояние с одним L.
Для разных приложений требуется разное. Если нужно просто угловой момент, или в случае электронов просто большой магнитнй момент, то достаточна и суперпозиция. Если нужны эффекты когерентности в поперечной плоскости, то нужно одномодовое состояние. Если нужна тонко настроенная суперпозиция, как например для квандового запутывания двух фотонов в многомерном пространстве собственных состояний с разными L, то опять же контроль должен быть на уровне отдельных L.
Спасибо. Про угловой момент понятно, он точно определен. А разве по радиальной координате не суперпозиция, ведь у пучка есть конечная радиальная ширина?
ОтветитьУдалитьЭто уже зависит от состояния. Если это чистое бесселево монохроматическое состояние, то у него фиксированы частота, z-компонента волнового вектора, азимутальная компонента — а значит, и радиальная тоже. По радиальной координате это получается чистый бессель, это и есть собственное состояние радиального волнового уравнения в цилиндрических координатах. Тут суперпозиции нет. (Имеется в виду, суперпозиции цилиндрических состояний, а не суперпозиции плоских волн.)
УдалитьНо чистый бессель во всем пространстве, конечно, нефизичен, он ненормируем. Поэтому реальные закрученные состояния, которые получают в эксперименте, являются суперпозициями с некоторой размазкой по z-компоненте и как следствие по радиальному состоянию. Конкретно, в эксперимента проще всего получаются вполне определенные суперпозиции — лагерр-гауссовы состояния. В них распределение интенсивности уже зависит от z-координаты (пучок сходится, а потом расходится), но от времени по-прежнему не зависит, т.к. это состояние монохроматическое.
Если же говорить про ограниченное пространство, например про цилиндрический волновой, то там можно держать и чистое бесселево состояние, поскольку поверхности нулевой интенсивности — цилиндры. Тогда точно нет никакой суперпозиции (в базисе цилиндрических волн).
Спасибо, я так и думал. В резонаторах шепчущей галереи есть возможность избирательно возбуждать моду (или их суперпозицию) с заданным угловым моментом, радиальным и продольным возбуждением. при выходе из резонатора угловой момент сохраняется, и, казалось бы, можно получать состояния с очень большим угловым моментом (10^8 для холодных нейтронов, например), если это где-то существенно.
УдалитьОго. Вы хотите сказать, что там можно получить состояние с каким-то одним-единственным L? Если так, то это был бы источник закрученных нейтронов, а я про такое еще ничего не слышал. Поделитесь ссылками?
УдалитьNature Physics 6, 114 - 117 (2010) , New J. Phys. 12 113050 . задачу получить состояние с заданным L не ставилось, но это вполне возможно.
ОтветитьУдалитьСпасибо, посмотрю. Насчет фиксированного L было бы очень интересно. Поскольку холодные нейтроны в интерферометрических методах диагностики материалов, это может быть перспективно и чисто с практической точки зрения.
УдалитьОбсудим с товарищами экспериментаторами. Тема интересная. А где закрученный нейтрон мог бы быть особо полезен?
ОтветитьУдалитьГотового ответа у меня нет, т.к. над конкретными примерами с холодными нейтронами не думал (с высокоэнергетическими протонами и нейтронами предложения у меня есть, но там действительно энергии порядка сотен МэВ и выше, что пока что нереально). Но на мой взгляд, само по себе экспериментальное получение закрученных нейтронов — это вам тема для еще одной статьи в Nature Physics.
УдалитьБудем думать, спасибо за интересную тему
ОтветитьУдалитьВидел ваш обзор по 'экспериментам с антиводородом в коллаборациии ASACUSA. Возможно вам будет интересно узнать о другой коллаборации Gbar, целью которой является исследование гравитационных свойств антиводорода, для чего антиатомы предполагают охладить до температуры в микрокельвины. Особенность Gbar в том, что там предполагается использовать весьма нестандартные идеи. В отличии от других групп, Gbar предполагает получить положительные ионы Hbar+, охладить их и лишь на последнем этапе превратить в антиводород. Наиболее "прикольной" опцией в программе Gbar является исследование антиводорода, подпрыгивающего в долгоживущих квантовых состояниях в гравитационном поле над материальной поверхностью (как мячик). Существование таких состояний возможно благодаря чисто квантовому эффекту "квантового" или надбарьерного отражения. Штука- весьма впечатляющая воображение тех, кто впервые знакомится с квантовой механикой (и матерых экспериментаторов тоже). http://gbar.web.cern.ch/GBAR/
ОтветитьУдалитьarXiv:1103.2150
Не рекламы ради, а чисто интересная штучка
Да, любопытно.
УдалитьВопрос о скорости распространения тут уже был, выше. Но в ответе зачем-то присутствует групповая скорость. И поэтому рождается другой вопрос: характеризуется ли чистое (не пакет) вихревое состояние двумя различными скоростями: фазовой и групповой?
ОтветитьУдалитьГоворя о световой закрученной волне, попадались ли Вам экспериментальные измерения скорости?
Да.
УдалитьЕсть и более простой пример — любая одномодовая монохроматическая ЭМ волна в волноводе. У нее там две скорости, групповая (< c) и фазовая (> c), а их произведение дает c^2.
Таких экспериментальных данных по закрученным состояниям не знаю. Но это все однозначно следует из уравнений Максвелла. Если бы эти скорости были иными, это было проявлялось в виде сильных нарушений УМ в пустоте.
Пример с волноводом не вполне подходит. Там групповое поведение возникает из-за самоинтерференции или, по-другому, из-за влияния особых граничных условий или особой геометрии среды. Крученая волна может существовать и в пустом пространстве.
УдалитьМожет, я что-то упускаю, но из картинки винтового волнового фронта не видно никакой другой перодичности в направлении распространения, кроме периодичности с длиной волны. Но тогда откуда возникает групповая скорость, отличная от фазовой?
Вот именно — тут тоже самоинтерференция! Вы можете расписать закрученную волну по плоским волнам. Это будут плоские волны с одинаковой частотой, сходящиеся к оси z под разными углами. Закрученная волна — это их интерференционный паттерн. Для случая чистого бесселева состояния — это интерференционный паттерн, зависящий от z только в виде фазового множителя.
УдалитьДоказано ли строго, что бесселев луч, несущий закрученность, (идеальный) тоже не рассеивается? Как это доказывается? Хотя бы в общих чертах.
ОтветитьУдалитьНе будет ли справедливо говорить, что закрученный бесселев луч всё же не является строго бесселевым лучом?
Вы под «не рассеивается» подразумеваете «не расходится», «не расплывается»? Да, конечно. Это вопрос из серии — доказано ли, что плоская волна не расходится; это всё доказывается форулами. Только идеальный бесселев пучок, также как и идеальная плоская волна, является идеализацией. Все реальные пучки расходятся, потому что они излучаются устройством с ограниченной апертурой.
УдалитьПлоская волна не расплывается – да. Бесселев луч не расплывается – да. Закрученный бесселев луч... – есть сомнения.
УдалитьПожалуйста, какие-нибудь аргументы в пользу этого. Хоть формулами, хоть «на пальцах».
В бесселевом луче, в волновой функции факторизуются зависимости от азимутального угла, от радиального расстояния, и от z. зависимость от z появляется только в виде exp(ikz). Соответственно, распределение интенсивности волны в поперечной плоскости не зависит от z.
УдалитьМне кажется, что вы придаете какое-то не то значение слову «закрученный». В закрученном луче нет ничего, что физически вращается и потому как бы разбегается из-за центробежной силы.
Нет-нет. Не из-за «физического вращения». А из-за отсутствия осевой симметрии. Есть ощущение, что формулы для бесселева луча могут здесь стать непригодными.
УдалитьНу я вам уже написал формулу. Если хотите увидеть ее вживую, см. например http://arxiv.org/abs/arXiv:1101.1206 , раздел 2.1 про скалярные бесселевы пучки, раздел 2.2 про оптические.
УдалитьНасчет осевой симметрии. Интенсивность — это квадрат модуля в.ф. Сама в.ф. не обязана быть совершенно инвариантной относительно азимутальных вращений. Главное, чтоб она была собственным состоянием генератора таких вращений, а уж собственное число может быть нулевым или ненулевым, это не важно. Это все достаточно для того, чтобы интенсивность уже была строго инвариантна.
Спасибо
УдалитьСтатья по вашей ссылке – рисунок 2 в разделе 2.2 иллюстрирует ваш последний абзац.
УдалитьНа рисунке видно, что действительно, квадрат модуля волновой функции не зависит от угла ϕ. Зависит от угла только фаза в.ф.
То есть векторный потенциал электромагнитного поля (классический) не зависит от угла. Следовательно не зависит от угла и вектор B (заглянул в формулу ротора для цилиндрических координат).
Получается, фаза волны не зависит от угла ϕ.
Так ли?
Во-первых, для фотона еще примешивается поляризация. Эта поляризация устроена ой как сложнее, чем поляризация плоской волны. Здесь поляризационные параметры зависят от точки в пространстве, поэтому у нас имеется уже не число, а поле поляризационных параметров. В частности, вдоль оси z у нас имеется линия сингулярностей этого поля.
УдалитьИз этого вытекает, что для закрученного фотона нет абсолютно однозначного определения, что такое плоско поляризованная закрученная волна. Есть разные методы фиксации поляризации, у Сербо есть один вариант, я с ним не совсем согласен.
В-третьих, даже если вы фиксируете вектор электрического поля максимально плоским (т.е. везде есть только x-компонента поля), то у B-поля появляется не только y, но и z-компонента, которая зависит от угла. Это связано с тем, что локально вектор, нормальный к волновому фронту, не константа, а тоже меняется от точки к точке.
Это всё интересная тема, но тут надо просто садиться и писать аккуратно решения уравнений Максвелла для такого пучка.
Банальный вопрос - из чего состоит эта закрученная волна? Если это поле - то из чего состоит это поле?
ОтветитьУдалитьЭто уже практически внефизический вопрос. Почему вы считаете, что должно существовать какое-то простое наглядное объяснение тому, из чего состоит поле? Поле состоит из поля, это базовая концепция. Вот тут уже обсуждались вопросы такого сорта.
УдалитьПо моему самый физический вопрос - объяснить почему возникает это поле. Объяснение -"Поле состоит из поля" - означает так должно быть! Это как раз не физическое объяснение. Уже доказано, что вакуум не пуст, т.е. присутствует среда. Так чем тогда отличается эта среда(вакуум) с полем от среды без поля?
Удалить