Начну с одной «стандартной» задачи (рис.1).
На закрепленном круглом бревне радиуса R покоится палочка длины 2L и пренебрежимо малой толщины. Проскальзывания между бревном и палочкой нет, т.е. трение бесконечное. Палочку чуть-чуть толкнули, и она начала колебаться около положения равновесия. Дано ускорение свободного падения g. Найти частоту малых колебаний палочки.
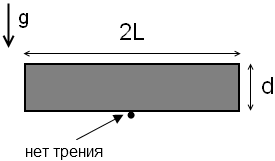
Эта задача может быть решена даже с помощью школьной механики. А вот теперь я дам задачу с условием как бы «наоборот» (рис.2).
На закрепленном круглом бревне пренебрежимо малого радиуса находится брусок длины 2L и ширины d. Трение между бревном и бруском отсутствует. Дано ускорение свободного падения g. Найти частоту малых колебаний около положения равновесия.
Вообще у этой задачи есть решение при произвольном соотношении L и d, но для простоты будем считать, что L много больше d. Какие будут идеи?
Апдейт: раскрываю комментарии! См. также обсуждение этой задачи на форуме linux.org.ru.
Апдейт 2: с задачей справился Rostik. Решение задачи идет отдельным постом.

так ведь упадет, если толкнуть!
ОтветитьУдалитьВот, возникает первый вопрос: где тут вообще колебательное движение?! Ищите :)
ОтветитьУдалитьСамый простой вариант более-менее устойчивых колебаний - стоячие акустические волны, хотя для них данных не хватает. Тоже самое с упругим колебанием концов, если приподнять брусок и отпустить.
ОтветитьУдалитьБрусок абсолютно жесткий. Здесь есть колебательный режим именно в движении бруска как целого.
ОтветитьУдалитьНаверно колебательный режим осуществляется так:
ОтветитьУдалитьТочку опоры смещают на dx и приподнимают брусок за длинный конец на dy. Тогда за половину периода он съедет на -2dx и противоположный конец поднимется на dy.
Как записывать уравнения я уже забыл :-(
Да, получаются колебания, хотя равновесие и неустойчивое. Если брусок сместить вправо и наклонить влево, то силы будут действовать в нужном напрпавлении. Но чтобы брусок не упал, начальный толчок должен быть строго выверен. Частота получается как sqrt(g/sqrt(m/I)), где I момент инерции бруска относительно точки касания с бревном.
ОтветитьУдалить99% перевалится через правый или левый край бруска.
ОтветитьУдалитьЦентр масс должен находиться точно над бревном, иначе колебаний не будет, а балка упадет. Т.к. трения нет, то ц.м. всегда будет точно над опорой.
ОтветитьУдалитьПолная энергия балки - это сумма кинетической энергии поступательного вертикального движения ц.м., кинетической энергии вращения балки относительно ц.м. и потенциальной энергии ц.м. в поле тяжести. Энергией поступательного движения можно пренебречь при малых колебаниях. Тогда получим:
ω^2 = 6gd/(4L^2+d^2) → 3gd/2L^2.
На самом деле, этот формальный ответ не совсем корректный, т.к. равновесие балки на опоре без трения неустойчиво - достаточно сместить центр масс на бесконечно малое расстояние от вертикали, проходящей через "бревно", и балка обязательно упадет. Правда, если это боковое смещение мало, балка успеет сделать некоторое число колебаний. Похожая некорректная задачка — найти частоту малых колебаний грузика, скользящего без трения по седловине.
Может нужно мыслить обратным образом: рассматривать колебания бруска относительно полочки?
ОтветитьУдалитьВо-первых, надо разобраться с малыми. Малым тут является угол колебаний, высота бруска и диаметр бревна. Вопрос в том, будут ли малы или велики отношения этих малых.
ОтветитьУдалитьВо-вторых, учитывая, что брусок скользит, то тут больше степеней свободы. Фактически, бесконечно тонкое (или пренебрежимо? есть ли разница?) бревно фиксирует лишь одну точку на поверхности бревна; вообще можно считать что это не бревно, а скользкое острие. А там уж бревно может и вращаться, и ездить влево и в право. Что делает задачу сложной, т.к. есть как минимум 4D пространство состояний (сдвиг, угол + линейная и угловые скорости). В общем, сложно сказать, будет ли оно тут УСТОЙЧИВО. Даже просто замкнутую траекторию тут найти затруднительно, мне в голову таких не приходит.
Кажется забыл указать, что такое I_0 ^-^.
ОтветитьУдалитьЗа I_0 принят момент инерции относительно середины длинного ребра.
to sitlar: я неправильно понял вначале, что Вы имели в виду. Точка опоры на бруске смещается на dx, да? Тогда возражений нет. :)
ОтветитьУдалитьТогда я сейчас другие ответы пооткрываю.
Насколько я понял, может установиться такой колебательный режим, когда движение доски будет похоже на движение больших качелей (лодка). При этом центр инерции будет описывать траекторию, похожую на параболу.
ОтветитьУдалитьДа, я имел ввиду систему отсчета связанную с ЦМ бруска.
ОтветитьУдалить> Т.к. трения нет, то ц.м. всегда
ОтветитьУдалить>будет точно над опорой.
Это не верно. На брусок действуют силы: сила тяжести (приложена к ЦМ и всегда вертикальна) и реакция опоры (приложена в точке, где брусок лежит на опоре, перпендикулярно скользкой поверхности). В сумме эти 2 силы и сдвигают, и поворачивают брусок с ненулевым ускорением. В итоге получаем весьма сложное движение, о котором писал выше.
Единственные малые колебания, которые я могу представить во второй системе, похожи на колебания в первой, с заменой R на d. Так что и ответ будет соответствующим.
ОтветитьУдалитьРешение чуть подробнее:
ОтветитьУдалитьВыберем две координаты для системы - смещение центра бруска с точки опоры - x и угол наклона бруска к горизонтали - a.
Выпишем уравнения движения оставив только члены первого порядка малости по x и a.
x" = ga
a" = mgx/I
I - момент инерции бруска относительно опоры.
В матричном виде:
|x|" |0 g| |x|
| |=| |*| |
|a| |mg/I 0| |a|
Собственные числе этой матрицы: L = (+/-)g*sqrt(m/I)
Положительное соответствует расходящемуся решению - соскальзыванию бруска. Отрицательное - колебательному движению. Круговая частота этих колебаний - корень из |L|, то есть w = sqrt(g*sqrt(m/I)).
Надо сначала без выбрасывания членов выяснить, существуют ли периодические решения.
ОтветитьУдалитьСтрого говоря, периодических решений нет, т.к. потенциальная энергия не имеет минимума.
ОтветитьУдалитьОтсутствие минимума потенциальной энергии не препятствует существованию периодических решений. Например, для грузика в седловине существуют периодические решения. Неустойчивые, но существуют! А какие имеются доводы, что для рассматриваемой здесь задачи существуют хотя бы какие-то периодические решения?
ОтветитьУдалитьПохожая задачка
ОтветитьУдалитьhttp://lanl.arxiv.org/abs/physics/0409154
Да-да, я собирался дать ссылку на эту статью после решения.
ОтветитьУдалить