Одна из таких задач -- поиск связанного состояния в двумерном потенциале нулевого радиуса. В одномерном случае такая задача решается влёт, а в двумерном приводит к совершенно нетривиальным явлениям типа перенормировки и понятию о том, что вообще значит правильно сформулировать задачу.
Вообще, это очень известная задача; она изучалась во многих статьях и самыми разными способами. Но поскольку в Рунете про эту задачу, насколько я вижу, ничего нет, то я подумал, что полезно будет в меру понятно и подробно рассказать о ней.
Рассказ будет состоять из трех постов: вводная часть, попытка решить задачу в лоб, и переформулировка задачи с ее последующим решением. Это не совсем популярные рассказы, но для студентов-физиков они могут показаться полезными.
Вступление
В физике встречаются задачи, в которых требуется описать взаимодействие волн вещества (электроны, нейтроны и т.д.) с сильными, но очень короткодействующими потенциалами (радиус действия потенциала много меньше длины волны частиц). Анализ таких задач показывает, что конкретный профиль потенциала тут обычно не существен, а важным является лишь единственное число, характеризуюшее силу потенциала в целом. В этом случае компактный потенциал со сложным профилем можно заменить просто дельта-функцией. Это резко упрощает вычисления при сохранении физической сути явления.
В качестве простейшего примера можно взять одномерную квантовомеханическую задачу о поиске связанного состояния в очень короткодействующем притягивательном потенциале с типичной глубиной −U0 и характерным радиусом действия a, для которого выполняется сильное неравенство
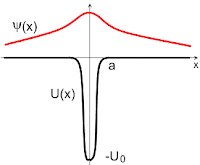 С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.
С одной стороны, известно, что в любом одномерном притягивательном потенциале имеется хотя бы одно связанное состояние. С другой стороны, ясно, что в данном случае это состояние не может поместиться внутрь потенциала, поскольку из-за выписанного выше неравенства кинетическая энергия частицы во много раз превысит потенциальную энергию. Поэтому это состояние будет в основном сидеть в пустом пространстве рядом с потенциалом и только чуть-чуть за него цепляться. Размер локализации частицы будет много больше a, и в первом приближении потенциал будет выглядеть для неё точечным, т.е. потенциалом нулевого радиуса.
Потенциалы нулевого радиуса (но с конечным интегралом) обычно описываются с помощью дельта-функций. Поэтому задачу о поиске связанного состояния в короткодействующем потенциале с хорошей точностью можно свести к решению уравнения Шредингера в одномерном дельта-функционном потенциале:
где
.
Как изучается буквально на самых первых семинарах по квантовой механике, в таком потенциале существует связанное состояние с энергией
Попытка провести те же самые рассуждения в двумерном случае -- то есть, промоделировать точечный потенциал с помощью двумерной дельта-функции -- неожиданно наталкивается на серьезные трудности. Разбираясь с ними, мы придем к необходимости переформулировать задачу и попутно увидим, как возникают некоторые очень интересные явления, про которые обычно упоминают только в курсах квантовой теории поля.
Оценки из соотношения неопределенностей
Прежде, чем приступать к честному решению задачи, полезно оценить энергию связанного состояния из соотношения неопределенностей. Вспомним, как это работает в одномерном случае.
У нас имеется потенциал с глубиной −U0 и шириной a, причем выполняется выписанное выше неравенство. Пусть Δx -- размер локализации волновой функции. Тогда энергию такого локализованного состояния можно оценить как
Для потенциальной энергии мы учли, что потенциал "ощущается" не всей волновой функцией, а только малой ее частью в области действия потенциала. Эта энергия имеет минимум при , и равна она
Из-за неравенства получается, что , т.е. уровень получается очень мелкий.
Попробуем записать то же в двумерном случае для потенциала глубиной −U0 и областью действия a в обоих направлениях.
Зависимость от Δx в кинетическом и потенциальном слагаемых получилась одинаковой. Это значит, что нам не удастся минимизировать потенциал ни при каких конечных Δx. То есть, с помощью такой оценки не удается "разглядеть", существует ли в таком потенциале связанное состояние или нет. (Более аккуратный подход показывает, что связанное состояние всегда есть, но с экспоненциально малой энергией связи.)
Итак, уже простые оценки показывают, что в случае двумерного потенциала нулевого радиуса нас ожидают какие-то сюрпризы. В следующем посте мы попробуем решить эту задачу честно и увидим, на каком именно этапе у нас возникают проблемы.
Куда так надолго пропали? Где можно посмотреть запись вашего выступления?
ОтветитьУдалитьИнтересно почитать также ваши комментарии по поводу
1) 22 июля 2009 года — полное солнечное затмение http://elementy.ru/news?newsid=431119
2) Запуск LHC откладывается еще на несколько недель http://elementy.ru/LHC/news?theme=2653111#n431122
> Куда так надолго пропали?
ОтветитьУдалитьДела, дела :)
> Где можно посмотреть запись вашего выступления?
Когда обработают, то вроде бы выложат на "Элементах". Но когда это будет, не знаю.
> 1) 22 июля 2009 года — полное солнечное затмение
А что тут комментировать? Затмение -- оно и есть затмение.
> 2) Запуск LHC откладывается еще на несколько недель
Ну так я эту заметку и написал. В качестве комментария я могу только повторить свое удивление тем, насколько инженеры недооценили техническую сложность такой установки, как LHC, и не обеспечили тотальный контроль качества во всех узлах еще в процессе изготовления и сборки.
Возможно, что гамильтониан рассматриваемой задачи не является самосопряженным и поэтому для корректного рассмотрения необходимо произвести его самосопряженное расширение.
ОтветитьУдалитьНу да, верно, с точки зрения высокой теории именно самосопряженное расширение и строится. Но я про это писать не буду, я напишу более физический подход через регуляризацию и перенормировку.
ОтветитьУдалить